

Instead, they are always found in either groups of three (baryons), or two (mesons). However, quarks are never found by themselves, due to a property called quark confinement. Quarks have a charge of $1\over 3$$e$, so that could be considered the minimum charge.
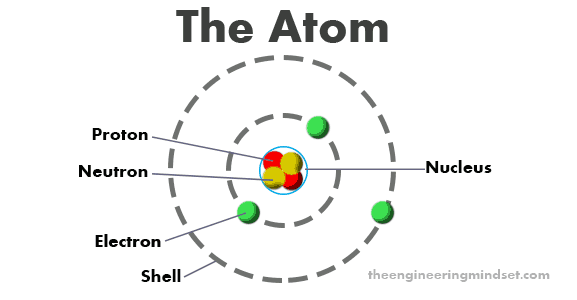
The electron charge is the minimum charge an isolatable particle can have. It's due to the observed fact that all charges come in common multiples of the electron charge.

Thus it would explain this equality.īy the way, bare charges of charged elementary particles are infinite and devoid of any physical meaning. This would turn an approximate equality in an exact equality, and hence prove the equality of the charges of the proton and the electron (apart from the sign). On the other hand, if a unified field thoery with a semisimple gauge group were found to be valid, it would forces charge quantization, as there are only a discrete number of irreducible unitary representations (which define the possible quantum numbers = charges).

On the level of the standard model, the value of the charges of the up and down quark comes from simple arithmetic from those of the proton and neutron, and hence doesn't give an independent piece of information. But it is extremely well established experimentally, as even small deviations would add up to huge amounts of electricity in bulk matter. On the level of QED and above, the equality of the charges has no theoretical explanation. This is enough conspiratorial implausibility, that together with the experimental bound, you can say with certainty that the proton and electron have exactly the same charge. So in order to make the charge of the proton slightly different from the electron, you can't modify parameters in the standard model, you need to add a heck of a lot of unobserved nearly massless fermions with tiny U(1) charge. I should point out that if you believe that the standard model matter is complete, then anomaly cancellation requires that the charge of the proton is equal to the charge of the positron, because there is instanton mediated proton decay as discovered by t'Hooft, and this is something we might concievable soon observe in accelerators. So in quantum gravity, the only alternative to charge quantization is a theory with nearly massless particles with extremely tiny charges, and this has clear experimental signatures. Further, in order for the theory to be consistent, a black hole made from the wee charges must be able to naturally decay to wee charged things, and barring a conspiratorial spectrum of charges and masses, this strongly suggests that the mass of the wee charges must be smaller than the charge, meaning that as the charge gets small they become massless. This means that in a consistent quantum gravity, you need either charge quantization or a spectrum of charges that accumulates near zero. If you have particle with charge q and a particle with charge q', and they aren't rational multiples of each other, you can produce a particle with charge $nq - m q'$ by throwing n q particles into a black hole, waiting for m q' particles to come out, and letting the resulting black hole decay, while throwing back any charge particle that comes out. It is also true that in any GUT theory producing electromagnetism, you get monopoles, so you automatically get charge quantization by Dirac's argument.īut even if you have a U(1) which is not part of a GUT, there are constraints from gravity. Breaking a compact group produces a subgroup, which is necessarily compact.
Proton charge quantity full#
This means that there is a gauge transformation by a full $2\pi$ rotation of the fields which is equivalent to nothing at all. In QED, charge quantization is equivalent to the statement that the gauge group is compact. If a proton could theoretically decay to a positron and neutral stuff, this is enough. To conclude that they are exactly equal requires an argument. It is an experimental fact that the proton and positron charges are very close. Because a proton can decay to a positron.


 0 kommentar(er)
0 kommentar(er)
